Tablas de contingencia

Las tablas de contingencia se utilizan para probar asociaciones entre dos o más variables categóricas. Los datos toman la forma de recuentos de observaciones que han sido clasificadas por estas variables categóricas.

Por ejemplo, considera los colores del pico y la cara del ave en peligro de extinción Gouldian Finch (Erythrura gouldiae) que vive en las sabanas del norte de Australia. Son polimórficos, teniendo caras de color rojo, amarillo o negro. Sus picos también son de color rojo, amarillo o negro, pero el color del pico no siempre es igual al color de la cara. Todas las aves en una muestra podrían ser clasificadas en las nueve combinaciones posibles de color de cara y color de pico, y los recuentos de cada combinación se mantendrían en una tabla bidimensional:

            Black face Red face Yellow face
Black bill          16        5           6
Red bill            19       20           6
Yellow bill         18       22          22

Para probar si una variable está asociada con la otra, contrastamos los recuentos observados con los recuentos esperados si no hubiera asociación (es decir, si las dos variables fueran completamente independientes entre sí). En este ejemplo, estaríamos probando si el color del pico varía de forma independiente al color de la cara.

Los recuentos esperados bajo este modelo nulo se calculan a partir de los totales de filas y columnas de la tabla que contiene los datos observados. Para cada celda de la tabla, el recuento esperado es:

(total de la fila x total de la columna) / total general

Cuando hacemos esto para cada celda, obtenemos una nueva tabla con todos los valores esperados:

            Black face  Red face Yellow face
Black bill    10.67910  9.470149    6.850746
Red bill      17.79851 15.783582   11.417910
Yellow bill   24.52239 21.746269   15.731343

Estos son los recuentos esperados si la hipótesis nula es verdadera. En este ejemplo, si el número de aves con cara negra, roja y amarilla está en las mismas proporciones para cada uno de los colores del pico.

Luego, los recuentos observados se contrastan con los recuentos esperados utilizando la estadística de prueba $\chi^2$.

$\chi^{2} = \sum_{i=1}^{k} \frac{(O_{i}-E_{i})^2}{E_{i}}$

donde O y E son los números observados y esperados en cada una de las celdas de la tabla.

Ejecutando el análisis

Con una calculadora, podrías calcular $\chi^2$ y luego determinar la probabilidad de obtener ese valor de $\chi^2$ a partir de una tabla de la distribución de probabilidad conocida de $\chi^2$. En R, podemos obtener esa probabilidad de la siguiente manera:

pchisq(x, df, lower.tail = FALSE)

con x = tu valor de $\chi^2$, y grados de libertad (df) = (número de filas-1) x (número de columnas-1). La parte lower.tail = FALSE te da la probabilidad de que $\chi^2$ sea mayor que tu valor.

Más fácil es ejecutar todo el análisis en R. Primero, debes ingresar las frecuencias observadas como una matriz.

Gfinch <- matrix(c(16, 19, 18, 5, 20, 22, 6, 6, 22), nrow = 3, dimnames = list(c("Black bill", "Red bill", "Yellow bill"), c("Black face", "Red face", "Yellow face")))

nrow le indica a R cuántas filas tienes. dimnames etiqueta las filas y columnas.

Verifica que has ingresado los datos correctamente simplemente ingresando el nombre de la matriz que acabas de crear.

Gfinch

Ejecuta el análisis de contingencia con la función chisq.test.

chisq.test(x, correct = F)

donde x es el nombre de la matriz que contiene los datos observados (para este ejemplo, usa el objeto Gfinch).

Interpretando los resultados

La salida de una tabla de contingencia es muy simple: el valor de $\chi^2$, los grados de libertad y el valor p. El valor p proporciona la probabilidad de que tus frecuencias observadas provengan de una población donde la hipótesis nula era verdadera.


    Pearson's Chi-squared test

data:  Gfinch
X-squared = 12.881, df = 4, p-value = 0.01187

En este ejemplo, la probabilidad de que las frecuencias observadas provengan de una población donde la hipótesis nula era verdadera es 0.01187. Luego, rechazaríamos la hipótesis nula y concluiríamos que existe una asociación entre el color del pico y el color de la cara.

Es importante recordar que esto no está probando ninguna de las variables por separado (por ejemplo, si las aves de cara negra se encuentran más comúnmente que las aves de cara roja o amarilla), sino una asociación entre ambas variables (es decir, si el color del pico es independiente del color de la cara).

Para explorar qué celdas de la tabla tienen más observaciones de las esperadas o menos observaciones de las esperadas, observa los residuos estandarizados. Estos son las diferencias entre los valores observados y esperados, estandarizados por la raíz cuadrada de los valores esperados. Están estandarizados porque la comparación de las diferencias absolutas (observado - esperado) puede ser engañosa cuando el tamaño de los valores esperados varía. Por ejemplo, una diferencia de 5 a partir de una expectativa de 10 es un aumento del 50%, pero una diferencia de 5 a partir de una expectativa de 100 es solo un cambio del 5%.

chisq.test(Gfinch)$residuals

            Black face    Red face Yellow face
Black bill    1.628236 -1.45259188  -0.3250357
Red bill      0.284793  1.06130659  -1.6033875
Yellow bill  -1.317120  0.05441038   1.5804894

En este ejemplo, se puede observar que las aves con cara negra tienen más probabilidades de tener un pico negro de lo que se esperaría por casualidad, y menos probabilidades de tener un pico amarillo.

Supuestos a verificar

Independencia. La prueba de $\chi^2$ asume que las observaciones se clasifican en cada categoría de manera independiente entre sí. Esto es un problema de diseño de muestreo y generalmente se evita mediante el muestreo aleatorio. En este ejemplo, habría problemas si eligieras deliberadamente aves con una combinación de color de pico y cara que no estuviera presente en las aves ya muestreadas.

Tamaño de la muestra. La estadística $\chi^2$ solo se puede comparar de manera confiable con la distribución $\chi^2$ si los tamaños de muestra son lo suficientemente grandes. Debes verificar que al menos el 20% de las frecuencias esperadas sean mayores que 5. Puedes ver las frecuencias esperadas para cada categoría al agregar $expected al final de tu prueba de $\chi^2$. Por ejemplo,

chisq.test(Gfinch)$expected

Si este supuesto no se cumple, puedes combinar categorías (si tienes más de dos y tiene sentido hacerlo), realizar una prueba de aleatorización o considerar un modelo log-lineal.

Comunicación de los resultados

Escrito. Los resultados del análisis de una tabla de contingencia se pueden presentar fácilmente en el texto de la sección de resultados. Por ejemplo, “Hubo una asociación significativa entre el color del pico y el color de la cara de los pinzones Gouldianos ($\chi^2$ = 12.88, df = 2, P = 0.01).”

Visual. Los datos de recuento se presentan mejor en un gráfico de barras con los recuentos en el eje Y y las categorías en el eje X.

barplot(Gfinch, beside = T, ylab = "Count", xlab = "Face colour", col = c("black", "red", "yellow"))
legend("topright", inset = 0.15, c("Black bill", "Red bill", "Yellow bill"), pch = 15, col = c("black", "red", "yellow"))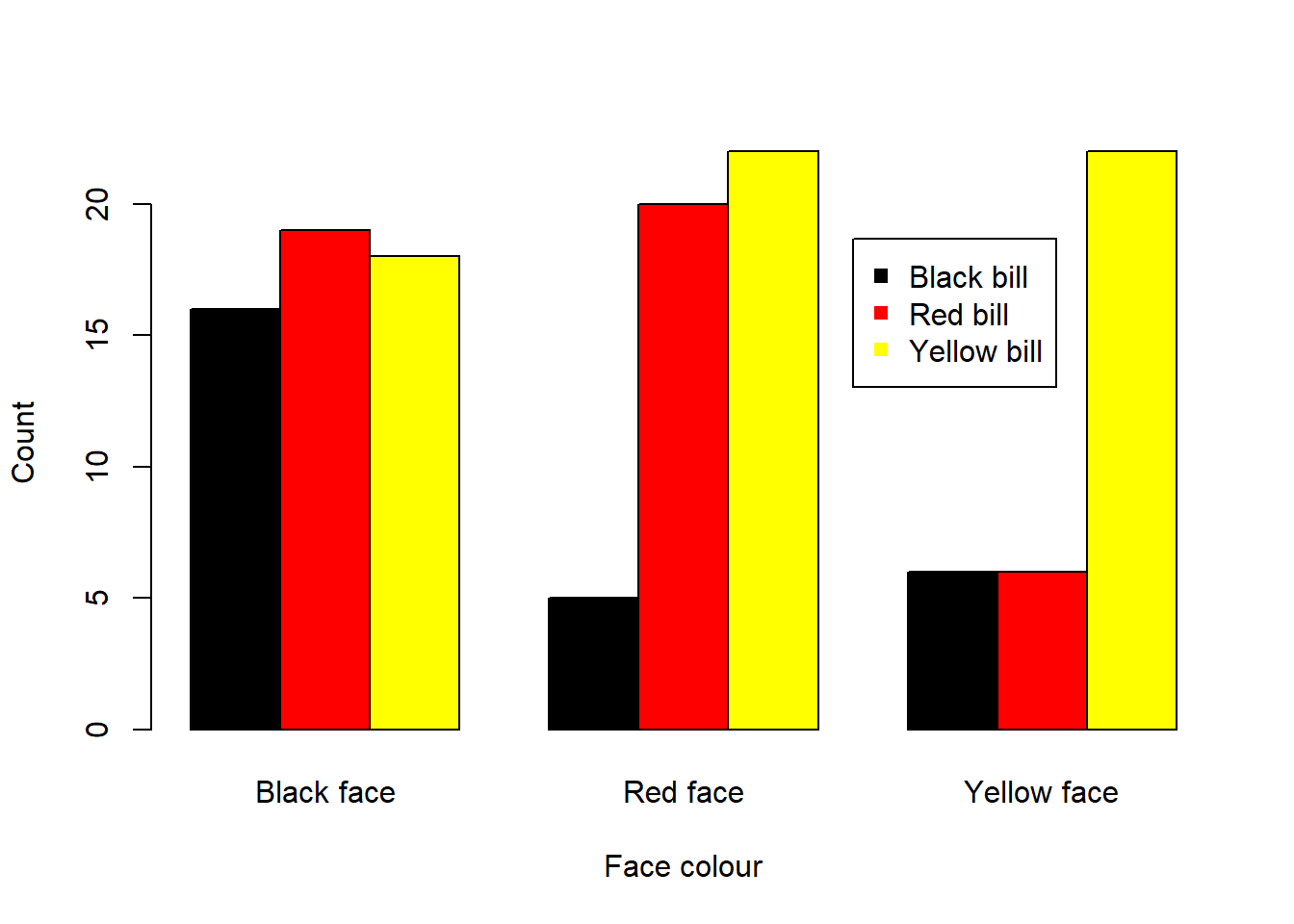

Consulta los módulos de visualización para obtener versiones mejoradas de estas figuras que sean adecuadas para informes o publicaciones.

Más ayuda

Escribe chisq.test para obtener la ayuda de R para esta función.

Quinn y Keough (2002) **Experimental design and data analysis for biologists*. Cambridge University Press. Capítulo 14. Análisis de frecuencias.

McKillup (2012) Statistics explained. An introductory guide for life scientists.. Cambridge University Press. Capítulo 20.3 Comparación de proporciones entre dos o más muestras independientes.

Autor: Alistair Poore

Año: 2016

Última actualización: Nov. 2023