Introducción

Modelos lineales mixtos con un efecto aleatorio

Necesitarás utilizar modelos de efectos mixtos si tienes un factor aleatorio en tu diseño experimental. Un factor aleatorio:

es categórico
tiene un gran número de niveles
solo se incluye una submuestra aleatoria de niveles en tu diseño
deseas hacer inferencia en general, no solo para los niveles que has observado.

Este es un concepto difícil de comprender y se explica mejor con un ejemplo. Los datos que analizaremos aquí son recuentos de invertebrados en 3-4 sitios de cada uno de los 7 estuarios (elegidos al azar). Aquí, los estuarios son el efecto aleatorio, ya que hay un gran número de estuarios posibles y solo tomamos una muestra aleatoria de algunos de ellos, pero nos gustaría hacer inferencias sobre los estuarios en general.

Introduciremos los modelos mixtos en tres partes:

Modelos mixtos 1 (esta página) es una introducción a los modelos mixtos para una variable respuesta continua con un efecto aleatorio. Aprenderás cómo verificar suposiciones y realizar inferencias, incluyendo el remuestreo paramétrico.
Modelos mixtos 2 amplía esto a múltiples efectos aleatorios con una respuesta continua. Exploraremos cómo modelar efectos aleatorios anidados y cruzados.
Modelos mixtos 3 te enseña cómo modelar datos discretos, incluyendo conteos y datos binarios, con efectos aleatorios.

Las tres páginas utilizarán los mismos datos para ilustración.

Propiedades de los modelos mixtos

Suposiciones. Los modelos mixtos tienen algunas suposiciones importantes (las revisaremos más adelante para nuestros ejemplos):

Las observaciones \(y\) son independientes, condicionales a algunos predictores \(x\).
La respuesta \(y\) sigue una distribución normal condicional a algunos predictores \(x\).
La respuesta \(y\) tiene una varianza constante, condicional a algunos predictores \(x\).
Existe una relación lineal entre \(y\) y los predictores \(x\) y los efectos aleatorios \(z\).
Los efectos aleatorios \(z\) son independientes de \(y\).
Los efectos aleatorios \(z\) siguen una distribución normal.

Ejecutando el análisis

Utilizaremos el paquete lme4 para todos nuestros modelos de efectos mixtos. Nos permitirá modelar tanto datos continuos como discretos con uno o más efectos aleatorios. Primero, instala y carga este paquete:

library(lme4)

Analizaremos un conjunto de datos que tuvo como objetivo probar el efecto de la contaminación del agua en la abundancia de algunos invertebrados marinos submareales, comparando muestras de estuarios modificados y prístinos. Como los recuentos totales son grandes, asumiremos que los datos son continuos. Más adelante, en Modelos mixtos 3, modelaremos los recuentos como discretos utilizando modelos lineales mixtos generalizados (GLMM).

Descarga el conjunto de datos de muestra, Estuaries.csv, y cárgalo en R.

Estuaries <- read.csv("Estuaries.csv", header = T)

Ajuste de un modelo con un efecto fijo y aleatorio

En este conjunto de datos, tenemos un efecto fijo (Modificación; modificado vs prístino) y un efecto aleatorio (Estuario). Podemos usar la función lmer para ajustar un modelo para cualquier variable dependiente con una distribución continua. Para ajustar un modelo para la abundancia total, usaríamos:

ft.estu <- lmer(Total ~ Modification + (1 | Estuary), data = Estuaries, REML = T)

donde Total es la variable dependiente (a la izquierda de ~), Modificación es el efecto fijo, y Estuario es el efecto aleatorio.

Observa que la sintaxis para un efecto aleatorio es (1|Estuario) - esto ajusta una intercepción diferente (por lo tanto, 1) para cada Estuario.

Este modelo se puede ajustar mediante máxima verosimilitud (REML=F) o máxima verosimilitud restringida (>REML=T). Para ajustar modelos, es mejor usar REML, ya que es menos sesgado (imparcial para muestras equilibradas), especialmente en muestras pequeñas. Sin embargo, para usar la función anova a continuación, necesitamos volver a ajustar con máxima verosimilitud.

Supuestos a verificar

Antes de examinar los resultados de nuestro análisis, es importante verificar que nuestros datos cumplan con los supuestos del modelo que utilizamos. Veamos todos los supuestos en orden.

Supuesto 1: Las observaciones \(y\) son independientes, condicionales a algunos efectos fijos \(x\) y efectos aleatorios \(z\)

No podemos verificar este supuesto, pero puedes asegurarte de que sea cierto tomando una muestra aleatoria dentro de cada nivel del efecto aleatorio en tu diseño experimental.

Supuesto 2: La respuesta \(y\) se distribuye normalmente, condicional a algunos predictores \(x\) y efectos aleatorios \(z\)

Este supuesto solo es crítico cuando tenemos un tamaño de muestra pequeño o datos muy sesgados. Podemos verificarlo con un gráfico cuantil-normal de los residuos.

qqnorm(residuals(ft.estu))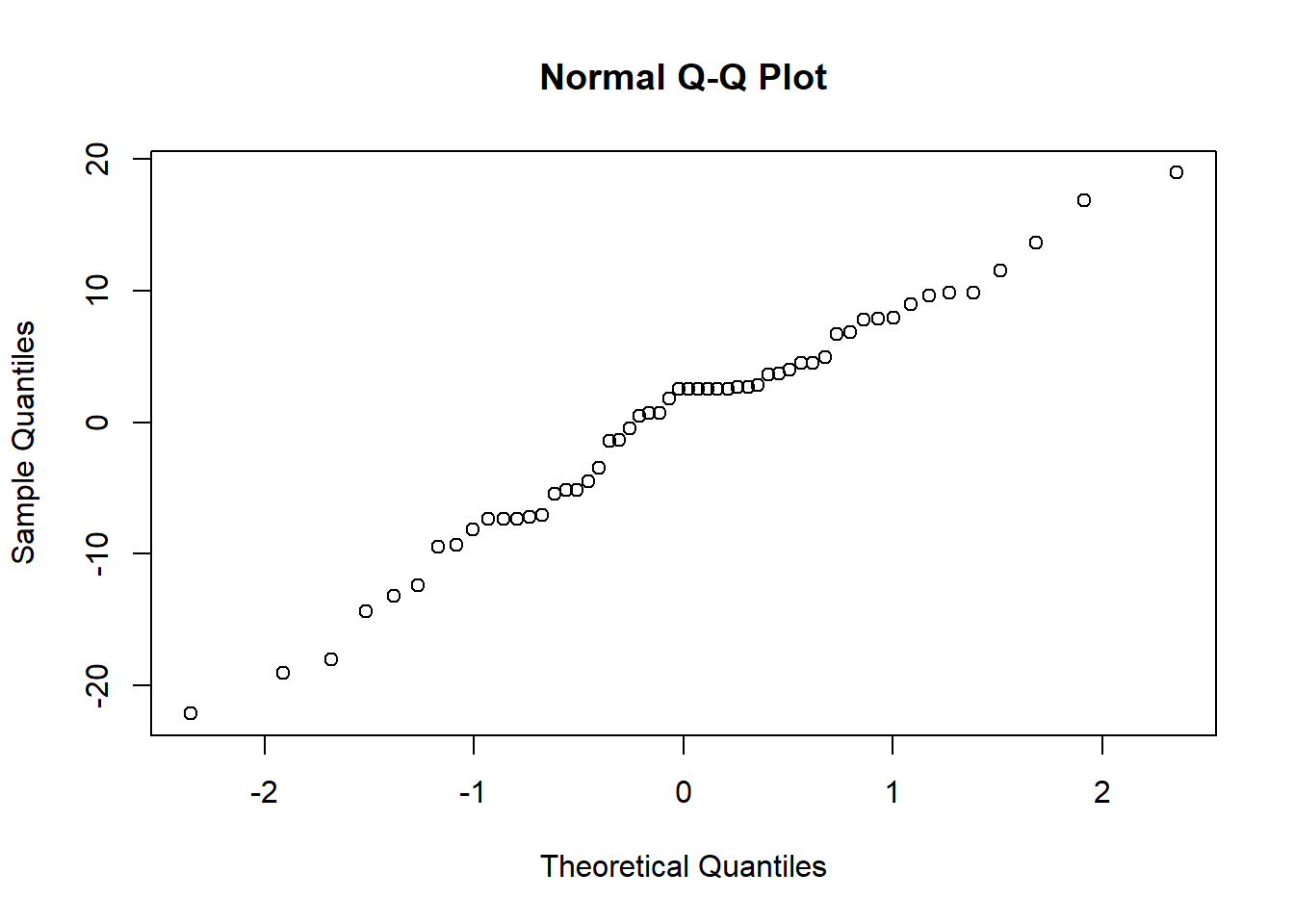

Estamos buscando una relación lineal. Aquí, la suposición de normalidad parece razonable.

Suposición 3: La respuesta \(y\) tiene varianza constante, condicional a algunos efectos fijos \(x\) y efectos aleatorios \(z\).

Al igual que en un modelo lineal, un modelo mixto asume una varianza constante. Podemos verificar esto buscando una forma de abanico en el gráfico de residuos (residuos vs valores ajustados).

scatter.smooth(residuals(ft.estu) ~ fitted(ft.estu))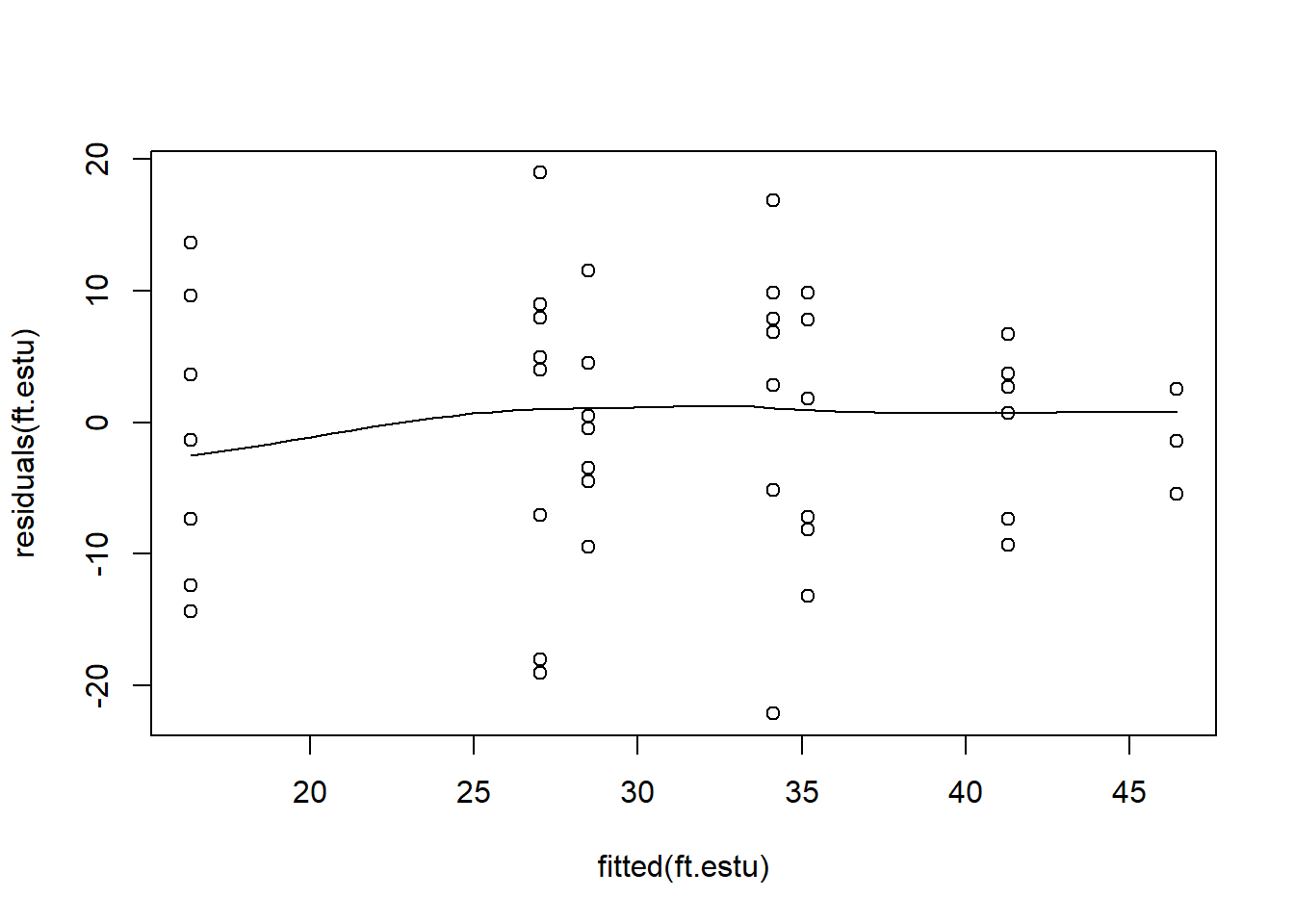

Este gráfico de residuos parece razonable, hay diferencias en la variabilidad entre estuarios, pero la variabilidad no aumenta con la media. Ten en cuenta que la función scatter.smooth es simplemente un gráfico de dispersión con una curva ajustada y suavizada.

Suposición 4: Existe una relación lineal entre \(y\) y los predictores \(x\) y los efectos aleatorios \(z\).

Para verificar esta suposición, revisamos nuevamente el gráfico de residuos en busca de no linealidad o forma de U. En nuestro caso, no hay evidencia de no linealidad. Si los residuos parecen ir hacia abajo y luego hacia arriba, o hacia arriba y luego hacia abajo, es posible que necesitemos agregar una función polinómica de los predictores utilizando la función poly.

Suposición 5: Los efectos aleatorios \(z\) son independientes de \(y\).

No podemos verificar esta suposición, pero puedes asegurarte de que sea verdadera tomando una muestra aleatoria de estuarios.

Suposición 6: Los efectos aleatorios \(z\) siguen una distribución normal.

Esta suposición no es crucial (y difícil) de verificar.

Interpretación de los resultados

Prueba de hipótesis para el efecto fijo

El paquete lme4 no proporcionará valores p para los efectos fijos como parte de la salida en summary. Esto se debe a que los valores p de las pruebas de Wald (usando summary) y las pruebas de razón de verosimilitud (usando anova) son solo aproximados en modelos mixtos.

No obstante, utilizaremos la función anova para probar un efecto de modificación en la abundancia total de invertebrados, teniendo en cuenta el efecto aleatorio del estuario.

Primero, ajustamos el modelo completo por máxima verosimilitud y un segundo modelo que carece del efecto fijo de la modificación.

ft.estu <- lmer(Total ~ Modification + (1 | Estuary), data = Estuaries, REML = F)
ft.estu.0 <- lmer(Total ~ (1 | Estuary), data = Estuaries, REML = F)

Entonces, comparamos estos dos modelos con una prueba de razón de verosimilitud utilizando la función anova.

anova(ft.estu.0, ft.estu)

Data: Estuaries
Models:
ft.estu.0: Total ~ (1 | Estuary)
ft.estu: Total ~ Modification + (1 | Estuary)
          npar    AIC    BIC  logLik deviance  Chisq Df Pr(>Chisq)  
ft.estu.0    3 415.02 420.99 -204.51   409.02                       
ft.estu      4 411.92 419.87 -201.96   403.92 5.1055  1    0.02385 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Encontramos evidencia de un efecto de Modificación (p = 0.02385).

También podemos calcular intervalos de confianza para cada parámetro del modelo utilizando la función confint.

confint(ft.estu)

Computing profile confidence intervals ...

                          2.5 %    97.5 %
.sig01                 2.718166 12.538348
.sigma                 7.676352 11.522837
(Intercept)           31.918235 49.981321
ModificationPristine -26.360731 -2.538241

Esto también proporciona evidencia de un efecto de Modificación, ya que este parámetro (es decir, la diferencia entre los estuarios modificados y prístinos) tiene intervalos de confianza del 95% que no se superponen con cero.

Prueba de hipótesis para efectos aleatorios

Puedes utilizar la función anova para probar efectos aleatorios, pero los valores p son muy aproximados y no recomendamos este procedimiento. En su lugar, utilizaremos un bootstrap paramétrico. Este es un método basado en simulación que implica una buena cantidad de código, pero no hay mucho sobre el código que debas cambiar para diferentes modelos, principalmente es solo cuestión de copiar y pegar.

Bootstrap paramétrico

nBoot <- 1000
lrStat <- rep(NA, nBoot)
ft.null <- lm(Total ~ Modification, data = Estuaries) # modelo nulo
ft.alt <- lmer(Total ~ Modification + (1 | Estuary), data = Estuaries, REML = F) # modelo alternativo
lrObs <- 2 * logLik(ft.alt) - 2 * logLik(ft.null) # estadístico de prueba observado
for (iBoot in 1:nBoot)
{
  Estuaries$TotalSim <- unlist(simulate(ft.null)) # datos remuestreados
  bNull <- lm(TotalSim ~ Modification, data = Estuaries) # modelo nulo
  bAlt <- lmer(TotalSim ~ Modification + (1 | Estuary), data = Estuaries, REML = F) # modelo alternativo
  lrStat[iBoot] <- 2 * logLik(bAlt) - 2 * logLik(bNull) # estadístico de prueba remuestreado
}
mean(lrStat > lrObs) # Valor p para la prueba del efecto de Estuario

[1] 0.001

Preguntas frecuentes sobre modelos mixtos

1. ¿Necesito muestras balanceadas para ajustar un modelo mixto?

No, los diseños no balanceados están bien. Sin embargo, los diseños balanceados generalmente te darán mejor poder estadístico, por lo que es bueno apuntar a ellos.

2. ¿Debo muestrear muchos niveles del efecto aleatorio o muchas observaciones dentro de cada nivel?

Esto depende de lo que te interese. En nuestro ejemplo, nos interesa el efecto de la modificación. En el diseño del estudio, las desembocaduras de los ríos se encuentran directamente debajo de la modificación, por lo que necesitamos muchas desembocaduras de ríos dentro de cada nivel de modificación para obtener una buena inferencia sobre los efectos de la modificación. Esto es cierto en general, necesitas muchas muestras en el nivel inferior al nivel que te interesa principalmente.

3. ¿Mi factor aleatorio debe ser un efecto aleatorio?

No necesariamente. Si tienes un factor aleatorio (es decir, tienes una muestra aleatoria de categorías de una variable categórica) y quieres hacer inferencias sobre esa variable en general, no solo en las categorías que observaste, entonces inclúyelo como un efecto aleatorio. Si estás satisfecho haciendo inferencias solo sobre los niveles que observaste, entonces puedes incluirlo como un efecto fijo. En nuestro ejemplo, queríamos hacer inferencias sobre la modificación en general, es decir, en cada desembocadura de río modificada y no modificada, por lo que incluimos la desembocadura de río como un efecto aleatorio. Si hubiéramos tratado la desembocadura de río como un factor fijo, nos habríamos limitado a hacer conclusiones solo sobre las desembocaduras de ríos que muestreamos.

4. ¿Qué pasa si los niveles de mi factor no son realmente aleatorios?

Esto podría ser un problema ya que la suposición 4 podría no cumplirse. Siempre debes muestrear el efecto aleatorio de manera aleatoria para evitar sesgos y conclusiones incorrectas.

Comunicación de los resultados

Escrita. Los resultados de los modelos mixtos lineales se comunican de manera similar a los resultados de los modelos lineales. En la sección de resultados, debes mencionar que estás utilizando modelos mixtos con el paquete R lme4, y listar tus efectos aleatorios y fijos. También debes mencionar cómo llevaste a cabo la inferencia, es decir, pruebas de razón de verosimilitud (usando la función anova) o bootstrap paramétrico. En la sección de resultados para un predictor, basta con escribir una línea, por ejemplo: “Hay evidencia sólida (p<0.001) de un efecto negativo de la modificación en la abundancia total”. Para múltiples predictores, es mejor mostrar los resultados en una tabla.

Visual. La mejor manera de comunicar visualmente los resultados dependerá de tu pregunta. Para un modelo mixto simple con un efecto aleatorio, una opción es un gráfico de los datos en bruto con las medias del modelo superpuestas. Se requiere un poco de código para este tipo de gráfico, y será un poco diferente para tus datos y modelo.

ModEst <- unique(Estuaries[c("Estuary", "Modification")]) # encontrar qué Estuarios están modificados

# Preparar un vector de colores con colores específicos para los niveles de modificación

myColors <- ifelse(unique(ModEst$Modification) == "Modified", rgb(0.1, 0.1, 0.7, 0.5),
  ifelse(unique(ModEst$Modification) == "Pristine", rgb(0.8, 0.1, 0.3, 0.6),
    "grey90"
  )
)

boxplot(Total ~ Estuary, data = Estuaries, col = myColors, xlab = "Estuary", ylab = "Total invertebrates")
legend("bottomleft",
  inset = .02,
  c(" Modified ", " Pristine "), fill = unique(myColors), horiz = TRUE, cex = 0.8
)

# 0 si está Modificado, 1 si está Prístino
is.mod <- ifelse(unique(ModEst$Modification) == "Modified", 0,
  ifelse(unique(ModEst$Modification) == "Pristine", 1, NA)
)

Est.means <- coef(ft.estu)$Estuary[, 1] + coef(ft.estu)$Estuary[, 2] * is.mod # Medias del modelo

Warning in coef(ft.estu)$Estuary[, 2] * is.mod: longitud de objeto mayor no es
múltiplo de la longitud de uno menor

stripchart(Est.means ~ sort(unique(Estuary)), data = Estuaries, pch = 18, col = "red", vertical = TRUE, add = TRUE)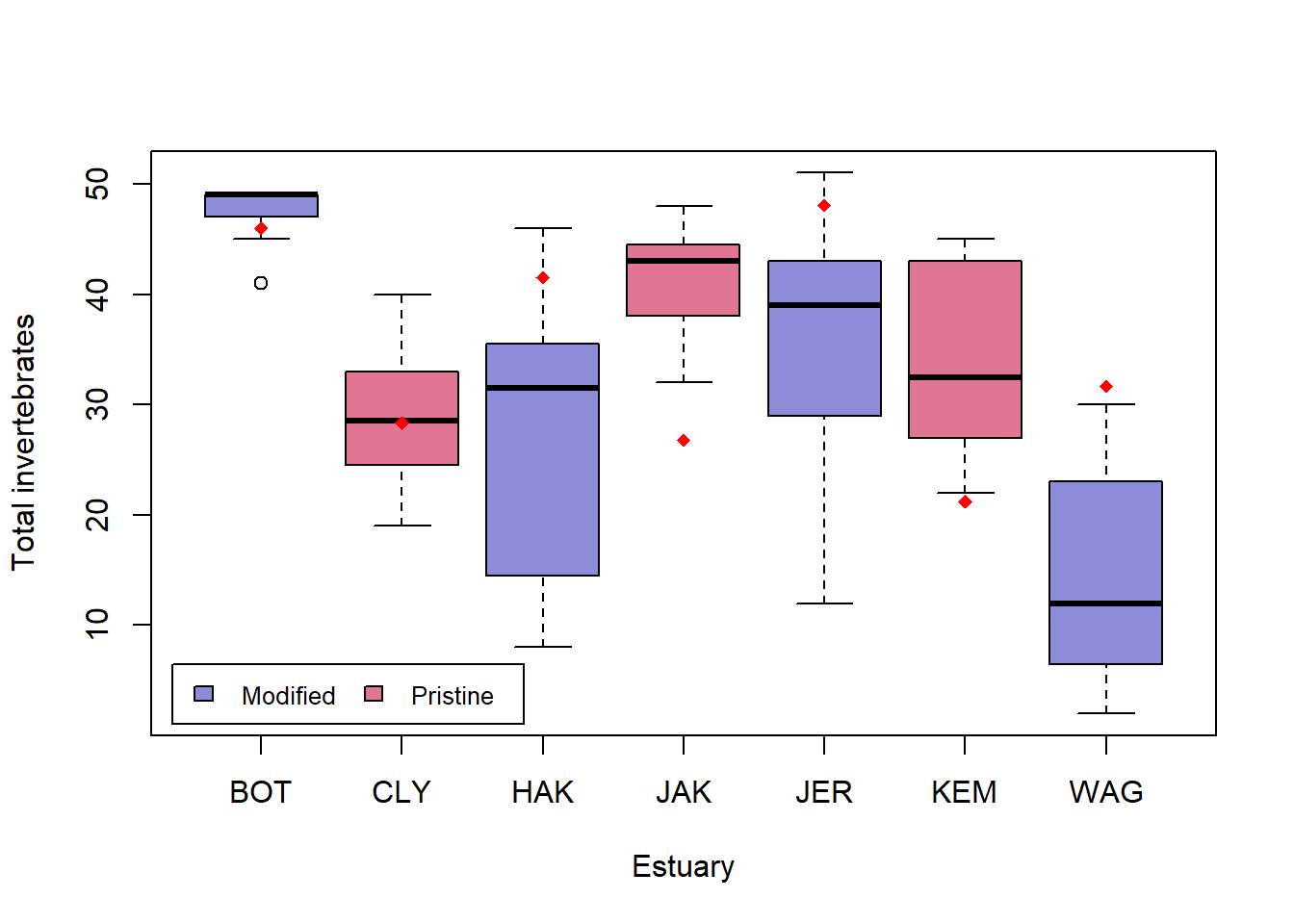

Más ayuda

Puedes escribir ?lmer en R para obtener ayuda con estas funciones.

Borrador de capítulo del libro de los autores de lme4.

Faraway, JJ. Extending the linear model with R: generalized linear, mixed effects and nonparametric regression models. CRC press, 2005.

Zuur, A, EN Ieno and GM Smith. Analysing ecological data. Springer Science & Business Media, 2007.

Autor: Gordana Popovic

Año: 2016

Última actualización: Nov. 2023