Prueba de una muestra con t de Student

Una de las pruebas de hipótesis más simples en estadística consiste en evaluar si un parámetro único obtenido de una muestra de mediciones difiere de un parámetro poblacional hipotético. La prueba busca determinar la probabilidad de obtener esa muestra a partir de una población con ciertas propiedades.

Para esto, utilizamos una prueba de una muestra con t de Student. La estadística de prueba, t, tiene la siguiente forma general:

\[t = \frac{St-\theta}{S_{St}}\]

Donde St es el valor de la estadística de tu muestra, \(\theta\) es el valor poblacional con el que estás comparando tu muestra, y \(S_{St}\) es el error estándar de tu estadística de muestra.

Estas pruebas se pueden utilizar para una variedad de parámetros muestreados de poblaciones (por ejemplo, medias, pendientes e interceptos en regresión lineal, etc.). Aquí, veamos un ejemplo sencillo en el que probamos si la media de un conjunto de medidas replicadas difiere de un valor hipotético.

Imagina que un científico forense intentaba rastrear el origen de algunas muestras de suelo tomadas de huellas en una escena del crimen. Recogió 10 muestras y analizó la concentración de polen de una especie de pino que se encuentra en un bosque local. Se sabía que el suelo de ese bosque local tenía una concentración promedio de 125 granos por gramo de suelo. La prueba de t de una muestra probará la probabilidad de que las diez muestras provengan de ese bosque al comparar la concentración promedio en las diez nuevas muestras con el valor esperado si provinieran de ese bosque.

La estadística de prueba, t, es:

\[t = \frac{\bar{x}-\mu}{SE}\]

donde \(\bar{x}\) es la media de la muestra, \(\mu\) es la media poblacional y SE es el error estándar de la muestra.

Ten en cuenta que el tamaño de la estadística de prueba depende de dos cosas: 1) qué tan diferente es la media de la muestra de la media poblacional (el numerador) y 2) cuánta variación está presente dentro de la muestra (el denominador). La hipótesis nula es que la media poblacional de la cual se tomó la muestra es el valor conocido, es decir, \(H_o: \mu=125\).

Ejecutando el análisis

La estadística de prueba t es relativamente sencilla de calcular manualmente. Luego, puedes comparar la estadística de prueba con una distribución t para determinar la probabilidad de obtener ese valor de la estadística de prueba si la hipótesis nula es verdadera.

Para calcular la probabilidad asociada a un valor dado de t en R, usa

pt(q, df = your.df, lower.tail = FALSE) * 2

donde q es tu valor de t, your.df son los grados de libertad (n-1). El lower.tail = FALSE asegura que estás calculando la probabilidad de obtener un valor de t más grande que el tuyo (es decir, la cola superior, P[X > x]). Ten en cuenta que el valor crítico para \(t_{\alpha = 0.05}\) varía según el número de grados de libertad: a mayor número de grados de libertad, menor es el valor crítico de t.

Es mucho más fácil utilizar la función t.test en R para obtener la estadística de prueba y su probabilidad asociada en una sola salida. Para una prueba de t de una muestra, usaríamos:

t.test(y, mu = your.mu)

donde y es un vector con tus datos de muestra y your.mu es el parámetro de la población con el que estás comparando la muestra.

En nuestro ejemplo de la escena del crimen, podríamos asignar nuestras diez mediciones a un objeto llamado “polen” y ejecutar el test de t en ese objeto.

pollen <- c(94, 135, 78, 98, 137, 114, 114, 101, 112, 121)
t.test(pollen, mu = 125)

Interpretación de los resultados

    One Sample t-test

data:  pollen
t = -3.0691, df = 9, p-value = 0.01337
alternative hypothesis: true mean is not equal to 125
95 percent confidence interval:
  97.20685 120.79315
sample estimates:
mean of x 
      109 

La salida de una prueba t de una muestra es fácil de interpretar. En la salida anterior, la estadística de prueba t es -3.0691 con 9 grados de libertad, y un valor de p bajo (p = 0.013). Por lo tanto, podemos rechazar la hipótesis nula y concluir que es poco probable que las muestras de suelo de la escena del crimen provengan del bosque de pinos cercano.

También se obtiene la media de la muestra (109) y el intervalo de confianza del 95% para la media de la población estimada a partir de esa muestra (este no se superpondrá con la media hipotetizada cuando la prueba sea significativa).

Supuestos a verificar

Las pruebas t son pruebas paramétricas, lo que implica que podemos especificar una distribución de probabilidad para la población de la variable de la cual se tomaron las muestras. Las pruebas paramétricas (y no paramétricas) tienen varios supuestos. Si se violan estos supuestos, no podemos estar seguros de que la estadística de prueba siga una distribución t, en cuyo caso los valores de p pueden ser inexactos.

Normalidad. La distribución t describe parámetros muestreados de una población normal, por lo que asume que los datos tienen una distribución normal. Sin embargo, hay que tener en cuenta que las pruebas t son bastante robustas ante violaciones de la normalidad (aunque hay que tener cuidado con la influencia de los valores atípicos).

Independencia. Las observaciones deben haber sido muestreadas al azar de una población definida para que la media de la muestra sea una estimación imparcial de la media de la población. Si los datos individuales están vinculados de alguna manera, se violará el supuesto de independencia.

Comunicación de los resultados

Escrito. Como mínimo, se debe informar la estadística de prueba t observada, el valor de p y el número de grados de libertad. Por ejemplo, se podría escribir “La media del recuento de polen de las huellas (109) fue significativamente más baja de lo esperado si proviniera del bosque cercano con un recuento promedio de 125 (t = 3.07, df = 9, P = 0.01)”.

Visual. Los diagramas de caja o histogramas de frecuencia se pueden utilizar para visualizar la variación en una sola variable. En este ejemplo, se podría utilizar una línea o una flecha para indicar el valor único (125) con el que se estaba comparando la muestra.

hist(pollen, xlab = "Pollen count", main = NULL)
abline(v = 125, col = "red")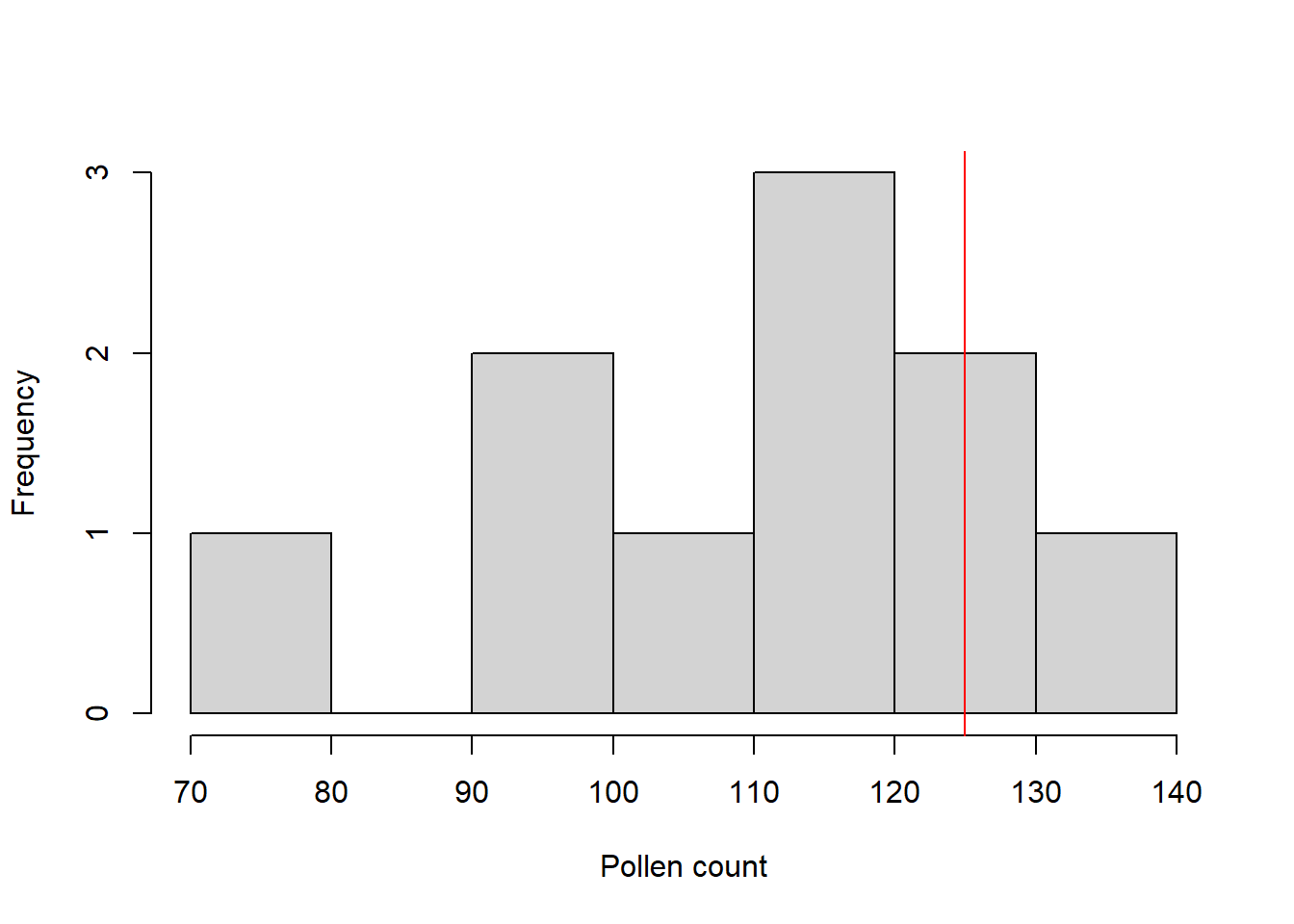

boxplot(pollen, xlab = "Pollen count", horizontal = TRUE)
abline(v = 125, col = "red")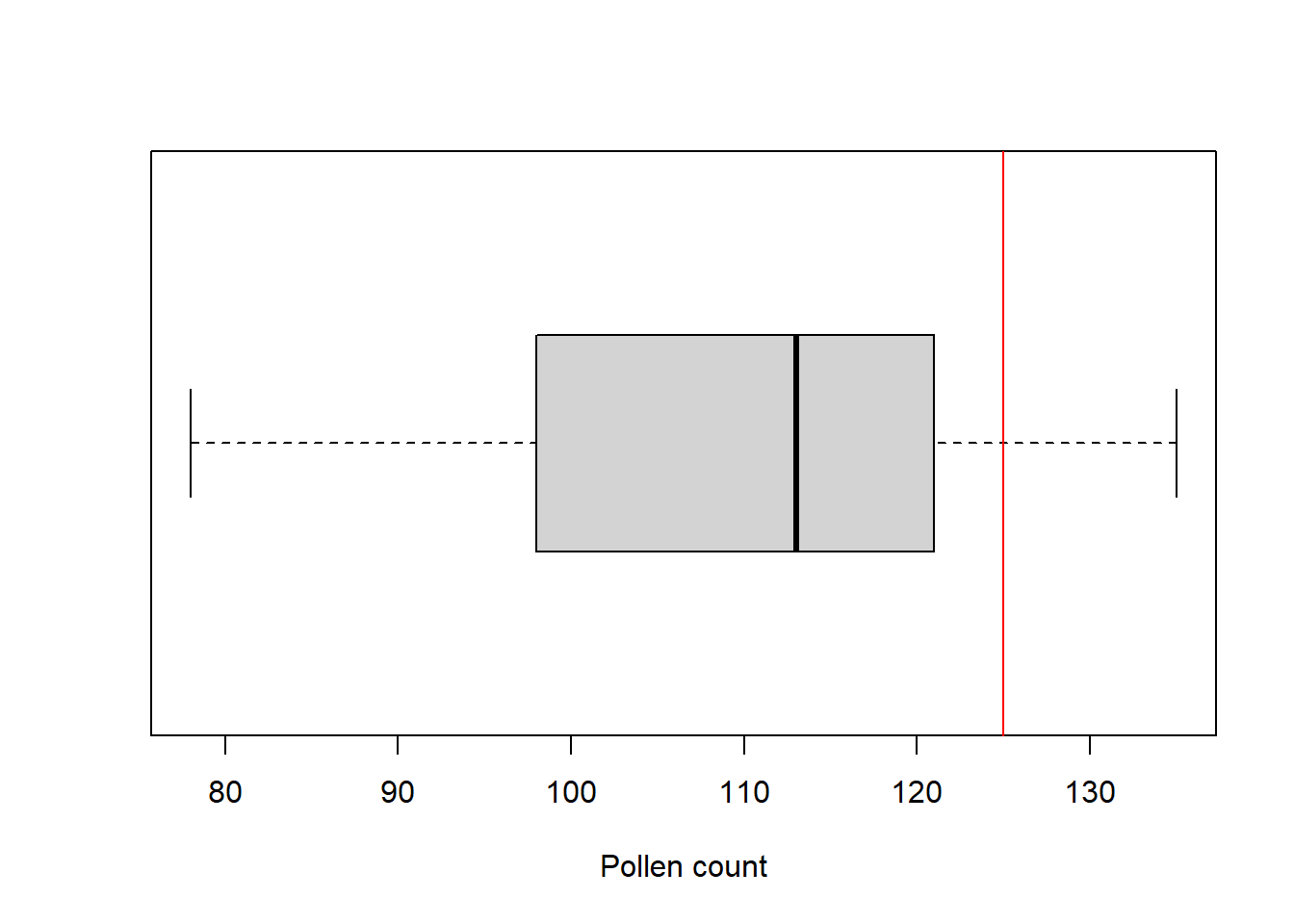

Más ayuda

Escribe ?t.test para obtener la ayuda de R sobre esta función.

Quinn and Keough (2002) **Experimental design and data analysis for biologists*. Cambridge University Press. Capítulo 3: Prueba de hipótesis.

McKillup (2012) Statistics explained. An introductory guide for life scientists. Cambridge University Press. Capítulo 9: Comparación de las medias de una y dos muestras de datos distribuidos normalmente.

Autor: Alistair Poore

Año: 2016

Última actualización: Nov. 2023